|
1,000,000,000,000
This list contains selected positive numbers in increasing order, including counts of things, dimensionless quantities and probabilities. Each number is given a name in the short scale, which is used in English-speaking countries, as well as a name in the long scale, which is used in some of the countries that do not have English as their national language. Smaller than (one googolth) * ''Physics:'' The probability of a human spontaneously teleporting due to quantum effects is approximately 10−4.5×1029. * ''Mathematics – random selections:'' Approximately is a rough first estimate of the probability that a typing "monkey", or an English-illiterate typing robot, when placed in front of a typewriter, will type out William Shakespeare's play ''Hamlet'' as its first set of inputs, on the precondition it typed the needed number of characters. However, demanding correct punctuation, capitalization, and spacing, the probability falls to around 10−360,783. * ''Compu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Long And Short Scales
The long and short scales are two power of 10, powers of ten number naming systems that are consistent with each other for smaller order of magnitude, numbers, but are contradictory for larger numbers. Other numbering systems, particularly in East Asia and South Asia, have large number naming that differs from both the long and short scales. Such numbering systems include the Indian numbering system and Chinese numerals, Chinese, Japanese numerals#Powers of 10, Japanese, and Korean Peninsula, Korean numerals. Much of the remainder of the world adopted either the short or long scale. Countries using the long scale include most countries in continental Europe and most that are Geographical distribution of French speakers, French-speaking, Geographical distribution of German speakers, German-speaking and Hispanophone, Spanish-speaking. Use of the short scale is found in most Anglophone, English and Arabic speaking countries, most Eurasian post-communist countries and Brazil. F ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Number
A number is a mathematical object used to count, measure, and label. The most basic examples are the natural numbers 1, 2, 3, 4, and so forth. Numbers can be represented in language with number words. More universally, individual numbers can be represented by symbols, called ''numerals''; for example, "5" is a numeral that represents the number five. As only a relatively small number of symbols can be memorized, basic numerals are commonly organized in a numeral system, which is an organized way to represent any number. The most common numeral system is the Hindu–Arabic numeral system, which allows for the representation of any Integer, non-negative integer using a combination of ten fundamental numeric symbols, called numerical digit, digits. In addition to their use in counting and measuring, numerals are often used for labels (as with telephone numbers), for ordering (as with serial numbers), and for codes (as with ISBNs). In common usage, a ''numeral'' is not clearly dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Card Shuffle
Shuffling is a technique used to randomize a deck of playing cards, introducing an element of chance into card games. Various shuffling methods exist, each with its own characteristics and potential for manipulation. One of the simplest shuffling techniques is the overhand shuffle, where small packets of cards are transferred from one hand to the other. This method is easy to perform but can be manipulated to control the order of cards. Another common technique is the riffle shuffle, where the deck is split into two halves and interleaved. This method is more complex but minimizes the risk of exposing cards. The Gilbert–Shannon–Reeds model suggests that seven riffle shuffles are sufficient to thoroughly randomize a deck, although some studies indicate that six shuffles may be enough. Other shuffling methods include the Hindu shuffle, commonly used in Asia, and the pile shuffle, where cards are dealt into piles and then stacked. The Mongean shuffle involves a specific seq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Decimal64 Floating-point Format
In computing, decimal64 is a decimal floating-point computer number format that occupies 8 bytes (64 bits) in computer memory. Decimal64 is a decimal floating-point format, formally introduced in the 2008 revision of the IEEE 754 standard, also known as ISO/IEC/IEEE 60559:2011. Format Decimal64 supports 'normal' values that can have 16 digit precision from to , plus 'denormal' values with ramp-down relative precision down to ±1.×10−398, signed zeros, signed infinities and NaN (Not a Number). This format supports two different encodings. The binary format of the same size supports a range from denormal-min , over normal-min with full 53-bit precision to max . Because the significand for the IEEE 754 decimal formats is not normalized, most values with less than 16 significant digits have multiple possible representations; 1000000 × 10−2=100000 × 10−1=10000 × 100=1000 × 101 all have the value 10000. These sets of representations for a same value are called '' c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Double-precision Floating-point Format
Double-precision floating-point format (sometimes called FP64 or float64) is a floating-point number format, usually occupying 64 bits in computer memory; it represents a wide range of numeric values by using a floating radix point. Double precision may be chosen when the range or precision of single precision would be insufficient. In the IEEE 754 standard, the 64-bit base-2 format is officially referred to as binary64; it was called double in IEEE 754-1985. IEEE 754 specifies additional floating-point formats, including 32-bit base-2 ''single precision'' and, more recently, base-10 representations (decimal floating point). One of the first programming languages to provide floating-point data types was Fortran. Before the widespread adoption of IEEE 754-1985, the representation and properties of floating-point data types depended on the computer manufacturer and computer model, and upon decisions made by programming-language implementers. E.g., GW-BASIC's double-precision ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
IEEE Floating-point
The IEEE Standard for Floating-Point Arithmetic (IEEE 754) is a technical standard for floating-point arithmetic originally established in 1985 by the Institute of Electrical and Electronics Engineers (IEEE). The standard addressed many problems found in the diverse floating-point implementations that made them difficult to use reliably and portably. Many hardware floating-point units use the IEEE 754 standard. The standard defines: * ''arithmetic formats:'' sets of binary and decimal floating-point data, which consist of finite numbers (including signed zeros and subnormal numbers), infinities, and special "not a number" values ( NaNs) * ''interchange formats:'' encodings (bit strings) that may be used to exchange floating-point data in an efficient and compact form * ''rounding rules:'' properties to be satisfied when rounding numbers during arithmetic and conversions * ''operations:'' arithmetic and other operations (such as trigonometric functions) on arithmetic format ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
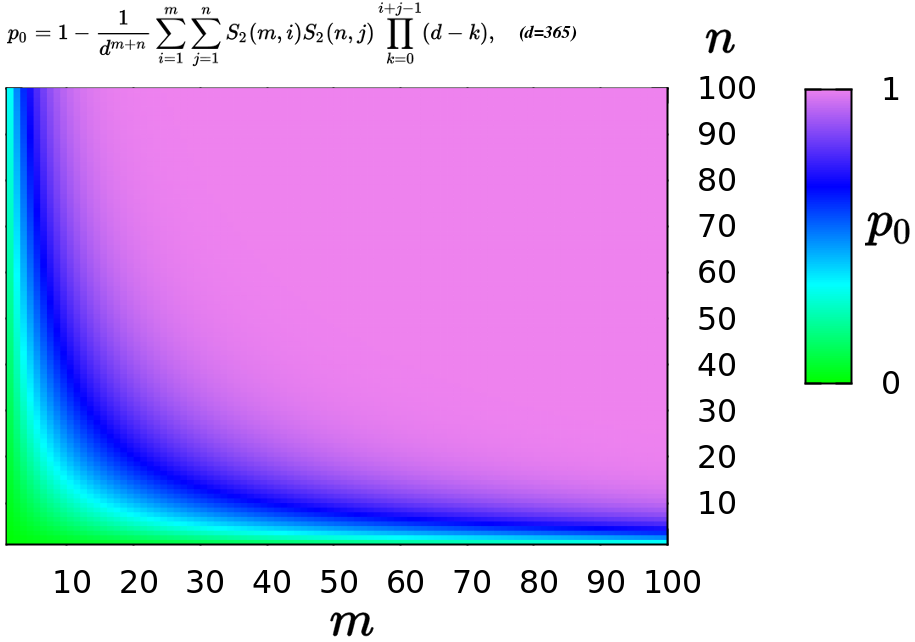
Birthday Problem
In probability theory, the birthday problem asks for the probability that, in a set of randomly chosen people, at least two will share the same birthday. The birthday paradox is the counterintuitive fact that only 23 people are needed for that probability to exceed 50%. The birthday paradox is a veridical paradox: it seems wrong at first glance but is, in fact, true. While it may seem surprising that only 23 individuals are required to reach a 50% probability of a shared birthday, this result is made more intuitive by considering that the birthday comparisons will be made between every possible pair of individuals. With 23 individuals, there are = 253 pairs to consider. Real-world applications for the birthday problem include a cryptographic attack called the birthday attack, which uses this probabilistic model to reduce the complexity of finding a Collision attack, collision for a hash function, as well as calculating the approximate risk of a hash collision existi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Decimal32 Floating-point Format
In computing, decimal32 is a decimal floating-point computer numbering format that occupies 4 bytes (32 bits) in computer memory. Purpose and use Like the binary16 and binary32 formats, decimal32 uses less space than the actually most common format binary64. Range and precision decimal32 supports 'normal' values, which can have 7 digit precision from up to , plus 'subnormal' values with ramp-down relative precision down to (one digit), signed zeros, signed infinities and NaN (Not a Number). The encoding is somewhat complex, see below. The binary format with the same bit-size, binary32, has an approximate range from subnormal-minimum over normal-minimum with full 24-bit precision: to maximum . Encoding of decimal32 values decimal32 values are encoded in a 'not normalized' near to 'scientific format', with combining some bits of the exponent with the leading bits of the significand in a 'combination field'. Besides the special cases infinities and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logarithmic Scale
A logarithmic scale (or log scale) is a method used to display numerical data that spans a broad range of values, especially when there are significant differences among the magnitudes of the numbers involved. Unlike a linear Scale (measurement), scale where each unit of distance corresponds to the same increment, on a logarithmic scale each unit of length is a multiple of some base value raised to a power, and corresponds to the multiplication of the previous value in the scale by the base value. In common use, logarithmic scales are in base 10 (unless otherwise specified). A logarithmic scale is Nonlinear system, nonlinear, and as such numbers with equal distance between them such as 1, 2, 3, 4, 5 are not equally spaced. Equally spaced values on a logarithmic scale have exponents that increment uniformly. Examples of equally spaced values are 10, 100, 1000, 10000, and 100000 (i.e., 101, 102, 103, 104, 105) and 2, 4, 8, 16, and 32 (i.e., 21, 22, 23, 24, 25). Exponential growt ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shuffling
Shuffling is a technique used to randomize a deck of playing cards, introducing an element of chance into card games. Various shuffling methods exist, each with its own characteristics and potential for manipulation. One of the simplest shuffling techniques is the overhand shuffle, where small packets of cards are transferred from one hand to the other. This method is easy to perform but can be manipulated to control the order of cards. Another common technique is the riffle shuffle, where the deck is split into two halves and interleaved. This method is more complex but minimizes the risk of exposing cards. The Gilbert–Shannon–Reeds model suggests that seven riffle shuffles are sufficient to thoroughly randomize a deck, although some studies indicate that six shuffles may be enough. Other shuffling methods include the Hindu shuffle, commonly used in Asia, and the pile shuffle, where cards are dealt into piles and then stacked. The Mongean shuffle involves a specific seq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Extended Precision
Extended precision refers to floating-point number formats that provide greater precision than the basic floating-point formats. Extended-precision formats support a basic format by minimizing roundoff and overflow errors in intermediate values of expressions on the base format. In contrast to ''extended precision'', arbitrary-precision arithmetic refers to implementations of much larger numeric types (with a storage count that usually is not a power of two) using special software (or, rarely, hardware). Extended-precision implementations There is a long history of extended floating-point formats reaching back nearly to the middle of the last century.. Various manufacturers have used different formats for extended precision for different machines. In many cases the format of the extended precision is not quite the same as a scale-up of the ordinary single- and double-precision formats it is meant to extend. In a few cases the implementation was merely a software-based change i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |