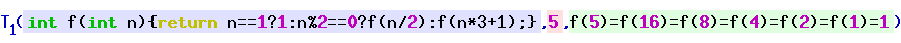|
Îś-recursive Function
In mathematical logic and computer science, a general recursive function, partial recursive function, or ÎĽ-recursive function is a partial function from natural numbers to natural numbers that is "computable" in an intuitive sense – as well as in a formal one. If the function is total, it is also called a total recursive function (sometimes shortened to recursive function). In computability theory, it is shown that the ÎĽ-recursive functions are precisely the functions that can be computed by Turing machines (this is one of the theorems that supports the Church–Turing thesis). The ÎĽ-recursive functions are closely related to primitive recursive functions, and their inductive definition (below) builds upon that of the primitive recursive functions. However, not every total recursive function is a primitive recursive function—the most famous example is the Ackermann function. Other equivalent classes of functions are the functions of lambda calculus and the functions tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Logic
Mathematical logic is the study of Logic#Formal logic, formal logic within mathematics. Major subareas include model theory, proof theory, set theory, and recursion theory (also known as computability theory). Research in mathematical logic commonly addresses the mathematical properties of formal systems of logic such as their expressive or deductive power. However, it can also include uses of logic to characterize correct mathematical reasoning or to establish foundations of mathematics. Since its inception, mathematical logic has both contributed to and been motivated by the study of foundations of mathematics. This study began in the late 19th century with the development of axiomatic frameworks for geometry, arithmetic, and Mathematical analysis, analysis. In the early 20th century it was shaped by David Hilbert's Hilbert's program, program to prove the consistency of foundational theories. Results of Kurt Gödel, Gerhard Gentzen, and others provided partial resolution to th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
ÎĽ Operator
In computability theory, the μ-operator, minimization operator, or unbounded search operator searches for the least natural number with a given property. Adding the μ-operator to the primitive recursive functions makes it possible to define all computable functions. Definition Suppose that R(''y'', ''x''1, ..., ''x''''k'') is a fixed (''k''+1)-ary relation on the natural numbers. The μ-operator "μ''y''", in either the unbounded or bounded form, is a " number theoretic function" defined from the natural numbers to the natural numbers. However, "μ''y''" contains a '' predicate'' over the natural numbers, which can be thought of as a condition that evaluates to ''true'' when the predicate is satisfied and ''false'' when it is not. The ''bounded'' μ-operator appears earlier in Kleene (1952) ''Chapter IX Primitive Recursive Functions, §45 Predicates, prime factor representation'' as: :"\mu y_ R(y). \ \ \mbox \ y [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kleene's T Predicate
In computability theory, the T predicate, first studied by mathematician Stephen Cole Kleene, is a particular set of triples of natural numbers that is used to represent computable functions within formal theories of arithmetic. Informally, the ''T'' predicate tells whether a particular computer program will halt when run with a particular input, and the corresponding ''U'' function is used to obtain the results of the computation if the program does halt. As with the smn theorem, the original notation used by Kleene has become standard terminology for the concept.The predicate described here was presented in (Kleene 1943) and (Kleene 1952), and this is what is usually called "Kleene's ''T'' predicate". (Kleene 1967) uses the letter ''T'' to describe a different predicate related to computable functions, but which cannot be used to obtain Kleene's normal form theorem. Definition The definition depends on a suitable Gödel numbering that assigns natural numbers to computable ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Church's Thesis
Church & Co Limited, branded Church's, is a luxury footwear manufacturer that was founded in 1873 by Thomas Church in Northampton, England. In 1999 the company was bought by Italian luxury fashion house Prada. Family Three brothers Alfred, (John) William, and (Thomas) Dudley formed the company; their father Thomas died on 23 March 1905. The granddaughter of Dudley was the Olympic swimmer Elizabeth Church. (Thomas) Dudley married Rhoda Wooding, daughter of Henry Wooding of Billing Road, at Victoria Road church on 3 January 1893. Alfred died on Saturday 29 September 1928 aged 77. He lived on Cheyne Walk, and attended Abington Avenue Congregational Church, where his funeral was held. Alfred had attended the church with Walter Drawbridge Crick, grandfather of Francis Crick. (John) William lived at Nine Springs Villa on Billing Road in Cliftonville, the former house of Walter Drawbridge Crick, until around 1928, when he moved to Leicester, where he died aged 76 on Thursday ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Halting Problem
In computability theory (computer science), computability theory, the halting problem is the problem of determining, from a description of an arbitrary computer program and an input, whether the program will finish running, or continue to run forever. The halting problem is ''Undecidable problem, undecidable'', meaning that no general algorithm exists that solves the halting problem for all possible program–input pairs. The problem comes up often in discussions of computability since it demonstrates that some functions are mathematically Definable set, definable but not Computable function, computable. A key part of the formal statement of the problem is a mathematical definition of a computer and program, usually via a Turing machine. The proof then shows, for any program that might determine whether programs halt, that a "pathological" program exists for which makes an incorrect determination. Specifically, is the program that, when called with some input, passes its own s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Total Turing Machine
In computability theory, a decider is a Turing machine that halts for every input. A decider is also called a total Turing machineKozen, 1997 as it represents a total function. Because it always halts, such a machine is able to decide whether a given string is a member of a formal language. The class of languages which can be decided by such machines is the set of recursive languages. Given an arbitrary Turing machine, determining whether it is a decider is an undecidable problem. This is a variant of the halting problem, which asks for whether a Turing machine halts on a specific input. Functions computable by total Turing machines In practice, many functions of interest are computable by machines that always halt. A machine that uses only finite memory on any particular input can be forced to halt for every input by restricting its flow control capabilities so that no input will ever cause the machine to enter an infinite loop. As a trivial example, a machine implementi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Junctor
A junctor is a circuit used in analog telephone exchanges, including the Number One Crossbar Switching System, Number Five Crossbar Switching System, 1ESS switch and other switches. In early electromechanical switches, a "district junctor" handled supervision and talk battery duties for outgoing calls, similar to the duties of the cord circuit of manual exchanges. The junctors for incoming calls were simple three-wire connections between the incoming frame and the line frame. In the later electromechanical 5XB switch The Number Five Crossbar Switching System (5XB switch) is a telephone switch for telephone exchanges designed by Bell Labs and manufactured by Western Electric starting in 1947. It was used in the Bell System principally as a Class 5 telephone swit ..., junctors only consisted of three wires to connect the two legs of a call: the line and the trunk, of which the latter supplied all talk battery and supervision. Stored-program analog switches such as the 1ESS sw ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logical Negation
In logic, negation, also called the logical not or logical complement, is an operation that takes a proposition P to another proposition "not P", written \neg P, \mathord P, P^\prime or \overline. It is interpreted intuitively as being true when P is false, and false when P is true. For example, if P is "Spot runs", then "not P" is "Spot does not run". An operand of a negation is called a ''negand'' or ''negatum''. Negation is a unary logical connective. It may furthermore be applied not only to propositions, but also to notions, truth values, or semantic values more generally. In classical logic, negation is normally identified with the truth function that takes ''truth'' to ''falsity'' (and vice versa). In intuitionistic logic, according to the Brouwer–Heyting–Kolmogorov interpretation, the negation of a proposition P is the proposition whose proofs are the refutations of P. Definition ''Classical negation'' is an operation on one logical value, typically th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer Square Root
In number theory, the integer square root (isqrt) of a non-negative integer is the non-negative integer which is the greatest integer less than or equal to the square root of , \operatorname(n) = \lfloor \sqrt n \rfloor. For example, \operatorname(27) = \lfloor \sqrt \rfloor = \lfloor 5.19615242270663 ... \rfloor = 5. Introductory remark Let y and k be non-negative integers. Algorithms that compute (the decimal representation of) \sqrt y run forever on each input y which is not a perfect square. The square roots of the perfect squares (e.g., 0, 1, 4, 9, 16) are integers. In all other cases, the square roots of positive integers are irrational numbers. Algorithms that compute \lfloor \sqrt y \rfloor do not run forever. They are nevertheless capable of computing \sqrt y up to any desired accuracy k. Choose any k and compute \lfloor \sqrt \rfloor. For example (setting y = 2): \begin & k = 0: \lfloor \sqrt \rfloor = \lfloor \sqrt \rfloor = 1 \\ & k = 1: \lfloor \sqrt \rfloo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Primitive Recursive Function
In computability theory, a primitive recursive function is, roughly speaking, a function that can be computed by a computer program whose loops are all "for" loops (that is, an upper bound of the number of iterations of every loop is fixed before entering the loop). Primitive recursive functions form a strict subset of those general recursive functions that are also total functions. The importance of primitive recursive functions lies in the fact that most computable functions that are studied in number theory (and more generally in mathematics) are primitive recursive. For example, addition and division, the factorial and exponential function, and the function which returns the ''n''th prime are all primitive recursive. In fact, for showing that a computable function is primitive recursive, it suffices to show that its time complexity is bounded above by a primitive recursive function of the input size. It is hence not particularly easy to devise a computable function th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Strong Equality
In mathematics Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ..., Kleene equality, or strong equality, (\simeq) is an equality operator on partial functions, that states that on a given argument either both functions are undefined, or both are defined and their values on that arguments are equal. For example, if we have partial functions f and g, f \simeq g means that for every x: * f(x) and g(x) are both defined and f(x) = g(x) * or f(x) and g(x) are both undefined. Some authors are using "quasi-equality", which is defined like this: (y_1 \sim y_2):\Leftrightarrow((y_1\downarrow \lor y_2\downarrow)\longrightarrow y_1=y_2), where the down arrow means that the term on the left side of it is defined. Then it becomes possible to define the strong equality in the following way: (f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |