|
(2,3,7) Triangle Group
In the theory of Riemann surfaces and hyperbolic geometry, the triangle group (2,3,7) is particularly important for its connection to Hurwitz surfaces, namely Riemann surfaces of genus ''g'' with the largest possible order, 84(''g'' − 1), of its automorphism group. The term "(2,3,7) triangle group" most often refers not to the full triangle group Δ(2,3,7) (the Coxeter group with Schwarz triangle (2,3,7) or a realization as a hyperbolic reflection group), but rather to the ordinary triangle group (the von Dyck group) ''D''(2,3,7) of orientation-preserving maps (the rotation group), which is index 2. Torsion-free normal subgroups of the (2,3,7) triangle group are Fuchsian groups associated with Hurwitz surfaces, such as the Klein quartic, Macbeath surface and First Hurwitz triplet. Constructions Hyperbolic construction To construct the triangle group, start with a hyperbolic triangle with angles π/2, π/3, and π/7. This triangle, the smallest hyperbolic Schwarz ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Riemann Surfaces
In mathematics, particularly in complex analysis, a Riemann surface is a connected one-dimensional complex manifold. These surfaces were first studied by and are named after Bernhard Riemann. Riemann surfaces can be thought of as deformed versions of the complex plane: locally near every point they look like patches of the complex plane, but the global topology can be quite different. For example, they can look like a sphere or a torus or several sheets glued together. Examples of Riemann surfaces include graphs of multivalued functions such as √''z'' or log(''z''), e.g. the subset of pairs with . Every Riemann surface is a surface: a two-dimensional real manifold, but it contains more structure (specifically a complex structure). Conversely, a two-dimensional real manifold can be turned into a Riemann surface (usually in several inequivalent ways) if and only if it is orientable and metrizable. Given this, the sphere and torus admit complex structures but the Möbius ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Fundamental Domain
Given a topological space and a group acting on it, the images of a single point under the group action form an orbit of the action. A fundamental domain or fundamental region is a subset of the space which contains exactly one point from each of these orbits. It serves as a geometric realization for the abstract set of representatives of the orbits. There are many ways to choose a fundamental domain. Typically, a fundamental domain is required to be a connected subset with some restrictions on its boundary, for example, smooth or polyhedral. The images of a chosen fundamental domain under the group action then tile the space. One general construction of fundamental domains uses Voronoi cells. Hints at a general definition Given an action of a group ''G'' on a topological space ''X'' by homeomorphisms, a fundamental domain for this action is a set ''D'' of representatives for the orbits. It is usually required to be a reasonably nice set topologically, in one of several ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hyperbolic Tilings
In hyperbolic geometry, a uniform hyperbolic tiling (or regular, quasiregular or semiregular hyperbolic tiling) is an edge-to-edge filling of the hyperbolic plane which has regular polygons as Face (geometry), faces and is vertex-transitive (Transitive group action, transitive on its vertex (geometry), vertices, isogonal, i.e. there is an isometry mapping any vertex onto any other). It follows that all vertices are Congruence (geometry), congruent, and the tessellation, tiling has a high degree of rotational and translational symmetry. Uniform tilings can be identified by their vertex configuration, a sequence of numbers representing the number of sides of the polygons around each vertex. For example, 7.7.7 represents the heptagonal tiling which has 3 heptagons around each vertex. It is also regular since all the polygons are the same size, so it can also be given the Schläfli symbol . Uniform tilings may be Regular polyhedron, regular (if also face- and edge-transitive), quasi- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
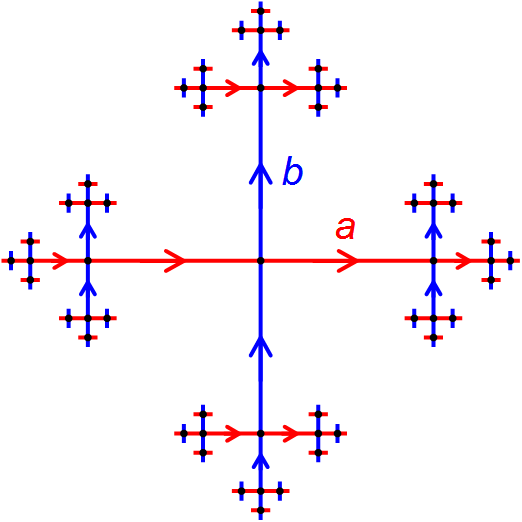
Geometric Group Theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups can act non-trivially (that is, when the groups in question are realized as geometric symmetries or continuous transformations of some spaces). Another important idea in geometric group theory is to consider finitely generated groups themselves as geometric objects. This is usually done by studying the Cayley graphs of groups, which, in addition to the graph structure, are endowed with the structure of a metric space, given by the so-called word metric. Geometric group theory, as a distinct area, is relatively new, and became a clearly identifiable branch of mathematics in the late 1980s and early 1990s. Geometric group theory closely interacts with low-dimensional topology, hyperbolic geometry, algebraic topology, computational group ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Journal Of Differential Geometry
The ''Journal of Differential Geometry'' is a peer-reviewed scientific journal of mathematics published by International Press on behalf of Lehigh University in 3 volumes of 3 issues each per year. The journal publishes an annual supplement in book form called ''Surveys in Differential Geometry''. It covers differential geometry and related subjects such as differential equations, mathematical physics, algebraic geometry, and geometric topology. The editor-in-chief is Shing-Tung Yau of Harvard University. History The journal was established in 1967 by Chuan-Chih Hsiung, who was a professor in the Department of Mathematics at Lehigh University at the time. Hsiung served as the journal's editor-in-chief, and later co-editor-in-chief, until his death in 2009. In May 1996, the annual Geometry and Topology conference which was held at Harvard University was dedicated to commemorating the 30th anniversary of the journal and the 80th birthday of its founder. Similarly, in May 2008 Ha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Systolic Geometry
In mathematics, systolic geometry is the study of systolic invariants of manifolds and polyhedra, as initially conceived by Charles Loewner and developed by Mikhail Gromov, Michael Freedman, Peter Sarnak, Mikhail Katz, Larry Guth, and others, in its arithmetical, ergodic, and topological manifestations. See also Introduction to systolic geometry. The notion of systole The ''systole'' of a compact metric space ''X'' is a metric invariant of ''X'', defined to be the least length of a noncontractible loop in ''X'' (i.e. a loop that cannot be contracted to a point in the ambient space ''X''). In more technical language, we minimize length over free loops representing nontrivial conjugacy classes in the fundamental group of ''X''. When ''X'' is a graph, the invariant is usually referred to as the girth, ever since the 1947 article on girth by W. T. Tutte. Possibly inspired by Tutte's article, Loewner started thinking about systolic questions on surfaces in the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Upper Half-plane
In mathematics, the upper half-plane, is the set of points in the Cartesian plane with The lower half-plane is the set of points with instead. Arbitrary oriented half-planes can be obtained via a planar rotation. Half-planes are an example of two-dimensional half-space. A half-plane can be split in two quadrants. Affine geometry The affine transformations of the upper half-plane include # shifts (x,y)\mapsto (x+c,y), c\in\mathbb, and # dilations (x,y)\mapsto (\lambda x,\lambda y), \lambda > 0. Proposition: Let and be semicircles in the upper half-plane with centers on the boundary. Then there is an affine mapping that takes A to B. :Proof: First shift the center of to Then take \lambda=(\text\ B)/(\text\ A) and dilate. Then shift to the center of Inversive geometry Definition: \mathcal := \left\ . can be recognized as the circle of radius centered at and as the polar plot of \rho(\theta) = \cos \theta. Proposition: in and are collinear points. In ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Modular Group
In mathematics, the modular group is the projective special linear group \operatorname(2,\mathbb Z) of 2\times 2 matrices with integer coefficients and determinant 1, such that the matrices A and -A are identified. The modular group acts on the upper-half of the complex plane by linear fractional transformations. The name "modular group" comes from the relation to moduli spaces, and not from modular arithmetic. Definition The modular group is the group of fractional linear transformations of the complex upper half-plane, which have the form :z\mapsto\frac, where a,b,c,d are integers, and ad-bc=1. The group operation is function composition. This group of transformations is isomorphic to the projective special linear group \operatorname(2,\mathbb Z), which is the quotient of the 2-dimensional special linear group \operatorname(2,\mathbb Z) by its center \. In other words, \operatorname(2,\mathbb Z) consists of all matrices :\begin a & b \\ c & d \end where a,b, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
SL(2,R)
In mathematics, the special linear group SL(2, R) or SL2(R) is the group of 2 × 2 real matrices with determinant one: : \mbox(2,\mathbf) = \left\. It is a connected non-compact simple real Lie group of dimension 3 with applications in geometry, topology, representation theory, and physics. SL(2, R) acts on the complex upper half-plane by fractional linear transformations. The group action factors through the quotient PSL(2, R) (the 2 × 2 projective special linear group over R). More specifically, :PSL(2, R) = SL(2, R) / , where ''I'' denotes the 2 × 2 identity matrix. It contains the modular group PSL(2, Z). Also closely related is the 2-fold covering group, Mp(2, R), a metaplectic group (thinking of SL(2, R) as a symplectic group). Another related group is SL±(2, R), the group of real 2 × 2 matrices with determinant ±1; this is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Morphing Of Modular Tiling To 2 3 7 Triangle Tiling
Morphing is a special effect in motion pictures and animations that changes (or morphs) one image or shape into another through a seamless transition. Traditionally such a depiction would be achieved through dissolving techniques on film. Since the early 1990s, this has been replaced by computer software to create more realistic transitions. A similar method is applied to audio recordings, for example, by changing voices or vocal lines. Early transformation techniques Long before digital morphing, several techniques were used for similar image transformations. Some of those techniques are closer to a matched dissolve – a gradual change between two pictures without warping the shapes in the images – while others did change the shapes in between the start and end phases of the transformation. Tabula scalata Known since at least the end of the 16th century, Tabula scalata is a type of painting with two images divided over a corrugated surface. Each image is only correctly vi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hurwitz Quaternion Order
The Hurwitz quaternion order is a specific order in a quaternion algebra over a suitable number field. The order is of particular importance in Riemann surface theory, in connection with surfaces with maximal symmetry, namely the Hurwitz surfaces. The Hurwitz quaternion order was studied in 1967 by Goro Shimura, but first explicitly described by Noam Elkies in 1998. For an alternative use of the term, see Hurwitz quaternion (both usages are current in the literature). Definition Let K be the maximal real subfield of \mathbb(\rho) where \rho is a 7th-primitive root of unity. The ring of integers of K is \mathbbeta/math>, where the element \eta=\rho+ \bar\rho can be identified with the positive real 2\cos(\tfrac). Let D be the quaternion algebra, or symbol algebra :D:=\,(\eta,\eta)_, so that i^2=j^2=\eta and ij=-ji in D. Also let \tau=1+\eta+\eta^2 and j'=\tfrac(1+\eta i + \tau j). Let :\mathcal_=\mathbbetai,j,j']. Then \mathcal_ is a maximal Order (ring theory), order ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Quaternion Algebra
In mathematics, a quaternion algebra over a field (mathematics), field ''F'' is a central simple algebra ''A'' over ''F''See Milies & Sehgal, An introduction to group rings, exercise 17, chapter 2. that has dimension (vector space), dimension 4 over ''F''. Every quaternion algebra becomes a matrix algebra by ''Scalar extension, extending scalars'' (equivalently, tensor product of algebras, tensoring with a field extension), i.e. for a suitable field extension ''K'' of ''F'', A \otimes_F K is isomorphic to the 2 × 2 matrix algebra over ''K''. The notion of a quaternion algebra can be seen as a generalization of Hamilton's quaternions to an arbitrary base field. The Hamilton quaternions are a quaternion algebra (in the above sense) over F = \mathbb, and indeed the only one over \mathbb apart from the 2 × 2 real number, real matrix algebra, up to isomorphism. When F = \mathbb, then the biquaternions form the quaternion algebra over ''F''. Structure ''Quat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |